Big O Notation Part 1
Big O notation was something that I always had a hard time in understanding. If you are like me, May be this post will clear some of the concepts. Let us start with what is algorithm complexity and why do we need them and what are the different way of finding complexity of an algorithm.
What is Algorithm Complexity
Algorithm Complexity is a way of measuring efficiency of an algorithm. There are 2 types of complexity usually consider while analysing an algorithm, which are time and space complexity.
Time complexity gives a rough estimation of number of steps an algorithm will run depending upon size of the input, while space complexity measures the amount of memory used by an algorithm to run.
In this article we will focus on time complexity specially Big O notation.
Why do we need it
Computer technology is evolving rapidly. A computer from 2008 will be slower than computers that we have today. A program will have different run time on different computer systems. Algorithm complexity helps to quantify an algorithm independent of the processing speed of a computer system.
Asymptotic Notation
Asymptotic Notations are mathematical expressions use to define complexity of an algorithm. It helps us in analysing the running time of an algorithm as the input size increases.
We can think of an algorithm as a function f with input size n, and f(n) as the running time of the algorithm. We can plot this function on a graph with y axis being the running time and x axis representing the input size. Following is an example of function f(n) = n log(n) +2
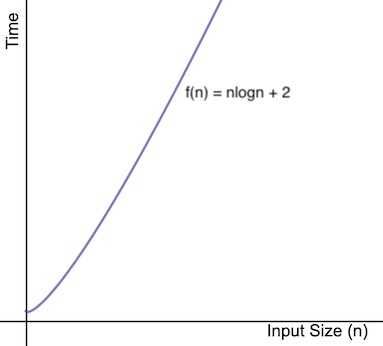
In asymptotic analysis, we try to find another function g(n) which is close to f(n). In Mathematics we call such curve as asymptotic curve,
We can analyse algorithm by its best, worst and average case, But Usually we focus on worst case.
Types of Asymptotic Notation
Big O
Big O is asymptotic notation for worst case. It gives tight upper bound on the growth rate of an algorithm. Let g(n) be a time complexity, The objective is to find smallest rate of growth, g(n), which is greater or equal to f(n). So we can say that, f(n) belongs to set of O(g(n)) if for some real constant c (c > 0) and n0 (n0>0), f(n) ≤ cg(n) for every input n (n>n0)
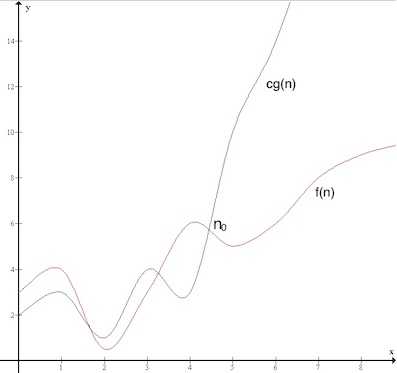
n0 is the point after which rate of growth is consider, n0 is called the threshold of the given function.
Big Omega Ω
Big omega is asymptotic notation for best case. It gives tight lower bound on the growth rate of an algorithm. Let g(n) be a time complexity, The objective is to find largest rate of growth g(n) which is less than equal to given function. f(n) belongs to set of Ω(g(n)) if for some real constant c (c > 0) and n0 (n0>0), f(n) ≥ cg(n) for every input n (n>n0)
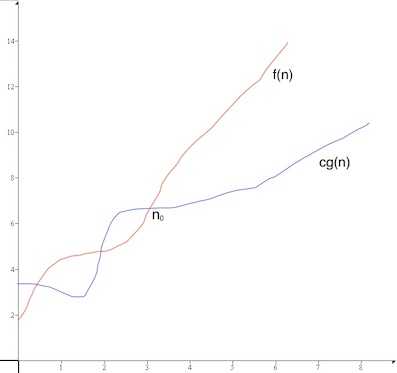
Theta θ
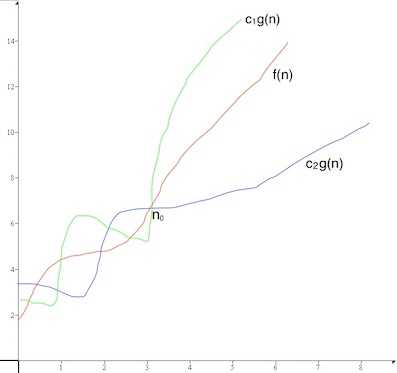
Theta is asymptotic notation for average case. Theta notation bounds the function from both above and below. It represents upper and lower bound of the function.
Let g(n) be a time complexity, f(n) belongs to the set θ(g(n)), if for some real constants c1 and c2 (c1, c2 > 0), c1g(n) < f(n) < c2g(n) for evenry input n (n > n0)
small o small o denotes loose upper bound on f(n). Let g(n) be a time complexity, f(n) belongs to set of o(g(n)), if f(n) < cg(n), for all constant c (c>0) and n (n > n0)
small omega ω small omega denotes loose lower bound on f(n). Let g(n) be a time complexity, f(n) belongs to set of o(g(n)), if f(n) > cg(n), for all constant c (c>0) and n (n > n0)
Difference between big O and small o notation
In big O, It is necessary to find a constant c for which the inequality holds
f(n) ≤ cg(n)
In little o, There is a minimum n0, after which inequality holds for all value of constant c (c>0)
f(n) < cg(n)
When we say f(n) ∈ O(g(n)), It means f’s asymptotic growth is no faster than g’s, On the other hand, when we say f(n) ∈ o(g(n)), It means f’s growth is strictly slower than g’s. Think of O as ≤ and o as <, which implies that if f(n) ∈ o(g(n)), than also f(n) ∈ O(g(n)). Therefore, there is a much larger gap between growth rate of f(n) and g(n) in small o as compared to big O.